Die Signalverarbeitung zur Halbbandfilter-Kaskade
Ein reelles Eingangssignal hat ein zu 0 Hz symmetrisches Spektrum und erstreckt sich zwischen der negativen und positiven halben Abtastfrequenz. In unserem Fall mit einem AD-Wandler, der mit 1 MHz abtastet kann man damit Signalfrequenzen bis zu 500 MHz erfassen.
Das ist das sogenannte Nyquist-Kriterium. Man braucht immer die doppelte Abtastfrequenz im Verhältnis zur Signalfrequenz um dieses Signal komplett zu erfassen. Tastet man zu niedrig ab, kommt es zu Frequenzspiegelungen. Diese könnten dem einen oder anderen aus der Optik bekannt sein. Wenn man ein Rad mit einem Strobtoskop beleuchtet und nehmen wir einmal an, dieses Rad hat eine deutliche Markierung (um die Symmetrie des Rades auszublenden). Dann sieht man die Rotation dieser Markierung. Wenn man jetzt die Geschwindigkeit des Rades erhöht, erhöht sich zuerst die empfundene Rotation des Rades, bis es dann wieder langsamer zu werden scheint und schließlich zum Stillstand kommt. Genau das ist eine Frequenzspiegelung. Den Stillstand erreicht man wenn die Signalfrequenz mit der Abtastfrequenz übereinstimmt, denn genau dann hat das Rad ja zwischen den Blitzen genau eine Umdrehung gemach und die Markierung erscheint wieder am gleichen Ort.
Jetzt wollen wir ja die Abtastrate verringern um uns das eigentliche Signal genauer anschauen zu können Dazu muss man wissen, dass bei der Unterabtastung um den Faktor zwei die Spektren von außen nach innen zurückgefaltet werden. Das bedeutet, dass die Frequenzen, die zuvor bei fs/2 waren sich denn mit denen von 0 überlagern. Es wird also das Spektrum von fs/4 bis fs/2 zu dem Spektrum von fs/4 bis 0 addiert.
Das in diesem Fall verwendete symmetrische Halbbandfilter hat einen Durchlassbereich und einen Sperrbereich die gleich groß sind. Möchte man z.B. Signale bis zu fs/8 ansehen, ist der Durchlassbereich fs/8 und der Sperrbereich ab fs/2 - fs/8. Wird auf diese Weise gefiltert so ist das Signal im Sperrbereich unterdrückt und man kann um den Faktor zwei unterabtasten, weil die Summe des Fehlers durch die Rückfaltung ja Null ist.
Für unsere Anwendung wollen wir ein Signal letztendlich mit knapp 4 kHz abtasten (dafür mit einer hohen Auflösung) und einen günstigen ADC bei hoher Abtastfrequenz verwenden. Das heißt am Ende haben wir noch ein Band bis 1,5 kHz übrig. Bei der ganzen Filterung, geht es nur darum, diese 1,5 kHz nicht zu korrumpieren. D.h. in der Filterkaskade muss der Durchlassbereich immer oberhalb dieser 1,5 kHz sein und der Sperrbereich 1,5 kHz unterhalb der jeweiligen fs liegen.
Hier sind die Frequenzgänge der Filter bezogen auf die ursprüngliche 1 MHz Abtastfrequenz:
Das Python-Programm zur Berechnung der Koeffizienten und der Frequenzgänge befindet sich im Repository.
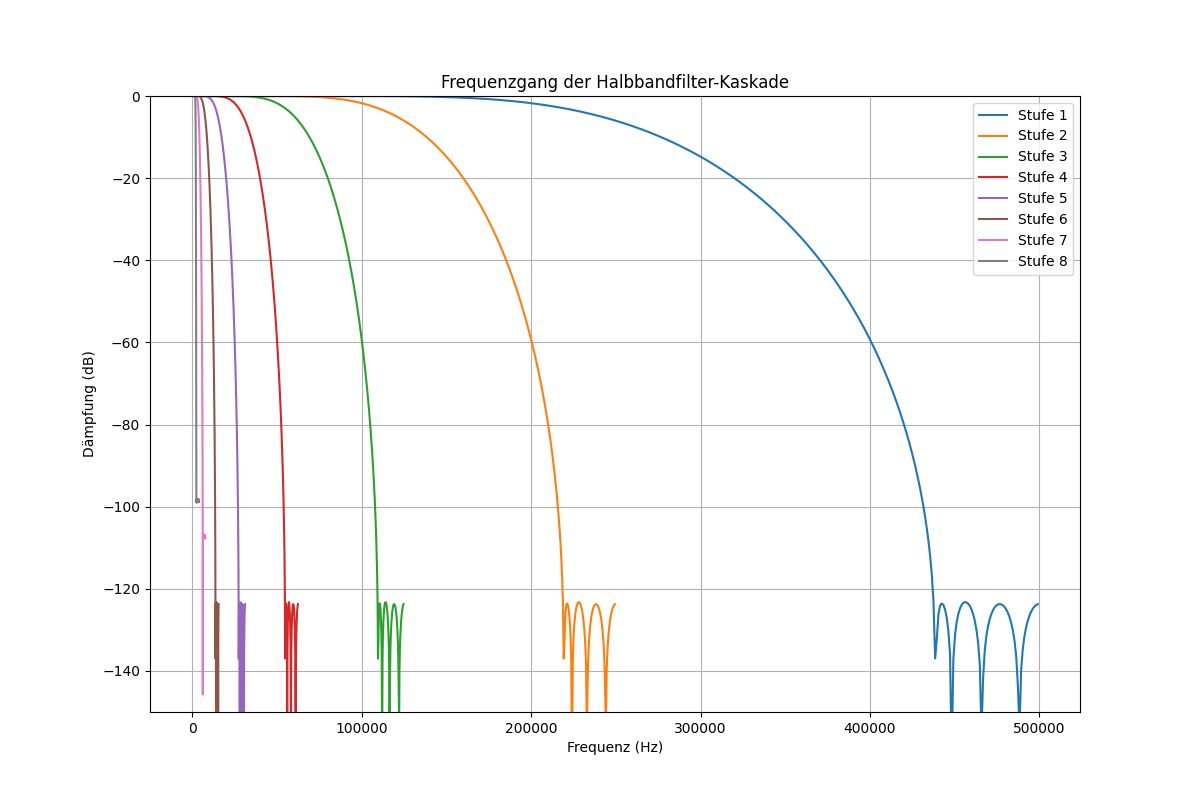
Man kann hier recht schön erkennen, wie von Stufe zu Stufe, der Sperrbereich unterdrückt wird und gespiegelt dazu der Durchlassbereich anscheinend unberührt davon bleibt.
Zusammenfassung
Wenn man in ein Frequenzband hineinzoomen möchte, muss man die Randbereiche des Spektrums unterdrücken, ohne das gewünschte Frequenzband zu verändern. Eine Effektive Möglichkeit dies zu erreichen ist die Halbbandfilterung mit anschließender Unterabtastung.
Dadurch mittelt man das interessierende Frequenzband auf und erreicht somit mehr Information pro Abtastwert, wodurch sich die Zunahme der Genauigkeit von 1 Bit pro zwei Stufen erklärt.
Das kann man auch sukzessive hintereinander machen um so in einer HBF-Kaskade stark in ein Band hineinzuzoomen.
Hier haben wir als Vorbereitung die acht Koeffizientensätze für die Halbbandfilter erstellt.
Weiter zur optimalen Struktur.


